通過計算得出了蒸發源位于倒圓錐面正下方外部鍍膜時錐面上各點的膜厚方程，并對整個錐面上膜厚均勻性進行了理論分析。結果表明：當圓錐面形狀固定時，蒸發源與圓錐底圓圓心距離增大使錐面上膜厚均勻性變好;當蒸發源固定時，增大底圓半徑導致錐面上膜厚均勻性變差。在同樣的配置下，蒸發源為點源或小平面源時錐面上膜厚均勻性的變化趨勢一致，小平面源蒸鍍比點源蒸鍍時圓錐面上膜厚均勻性差。

　　引言

　　真空鍍膜厚度均勻性對于各種薄膜制備是一個非常關鍵的因素。膜厚均勻性不僅能夠決定制備薄膜的面積，而且對于薄膜的各項性能都有重要影響。對于窄帶干涉、漸變濾光片等多層、高精度的光學薄膜，膜厚均勻性直接決定了濾光片制備的成敗，能否達到使用要求。真空鍍膜領域的研究者已經認識到膜厚均勻性的重要性，并研究了基片的溫度、基片的轉速、蒸發速率、蒸氣入射角、蒸發源的蒸發特性、蒸鍍系統的配置、修正板的幾何形狀等對薄膜均勻性的影響。然而對蒸發源的蒸發特性和蒸鍍系統配置這兩個最本質問題的研究主要集中在平面工件盤結構及球型表面，對于復雜表面如倒圓錐面等非平面鍍膜的研究比較少。通過計算得出了圓錐面形狀固定和蒸發源固定兩種情況下的膜厚理論分布，分析過程中將蒸發源分別作為兩類常見的蒸發源，即向四周均勻發射的點源和遵守余弦分布的小平面源。最后分析了實際蒸發源不同發射系數對形狀固定的倒圓錐面上膜厚均勻性的影響。

　　1、膜厚及膜厚均勻性方程

　　當蒸發源位于倒圓錐面正下方時，其蒸鍍配置如圖1所示，以圓錐底圓圓心O 為坐標原點建立坐標系，則圓錐底圓圓心O 坐標為(0，0，0);圓錐頂點Q 坐標為(0，0，-h)，h 為錐體高度;蒸發源S 坐標為(0，0，-L)，L 為蒸發源到圓錐底圓圓心的距離;圓錐底圓半徑為R。假設圓錐面上任意一點的坐標為A(x，y，z)，同時設z=-z0，則z0≥0，且0≤z0≤h。由于圓錐面關于z 軸對稱，故同一豎直高度錐面上鍍膜厚度相等，因此可選定x=0時圓錐面上的點來表示圓錐面上的任意點，則任意一點A 的坐標可表示為(0，y，-z0)，顯然該點滿足y=R(h-z0)/h。

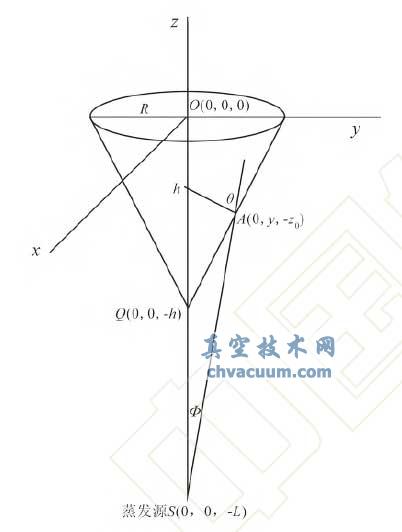
圖1 蒸發源位于錐形面正下方時蒸鍍配置圖

　　3、結論

　　主要對蒸發源位于倒圓錐面正下方的鍍膜均勻性進行了理論分析。通過計算得出了兩種常見理想蒸發源與實際蒸發源下，倒圓錐面的膜厚及膜厚均勻性方程，并分析了圓錐面形狀固定與蒸發源固定情況下的膜厚分布曲線。由此得出不同配置下圓錐面上各點的膜厚及整個圓錐面上的膜厚均勻性。該理論分析對于實際產品的研制具有一定的指導作用。